好像有点标题党。

学校最近更新了统一身份认证系统，从原来的明文传输密码变成了加密传输，安全性有了那么一点点提升（不过 HTTPS 依旧不是强制开启，所以并没有什么卵用）。然而这就导致了电表需要跟进新的登录方式，我也就得分析一下怎么加密的。

首先来看源代码，这里是我直接从 JS 里复制出来的：

function _gas(data, key0, iv0) {
    key0 = key0.replace(/(^\s+)|(\s+$)/g, "");
    var key = CryptoJS.enc.Utf8.parse(key0);
    var iv = CryptoJS.enc.Utf8.parse(iv0);
    var encrypted = CryptoJS.AES.encrypt(data, key, {
        iv: iv,
        mode: CryptoJS.mode.CBC,
        padding: CryptoJS.pad.Pkcs7
    });
    return encrypted.toString();
}

function encryptAES(data, _p1) {
    if (!_p1) {
        return data;
    }
    var encrypted = _gas(_rds(64) + data, _p1, _rds(16));
    return encrypted;
}

var $_chars = 'ABCDEFGHJKMNPQRSTWXYZabcdefhijkmnprstwxyz2345678';
var _chars_len = $_chars.length;
function _rds(len) {
    var retStr = '';
    for (i = 0; i < len; i++) {
        retStr += $_chars.charAt(Math.floor(Math.random() * _chars_len));
    }
    return retStr;
}

在加密密码的时候，调用的是 encryptAES(data, _p1) 函数，这里的 data 就是密码明文，_p1 是服务器生成的一个 16 字节的随机字符串。encryptAES 中生成一个 64 字节的随机字符串和密码明文拼接作为需要加密的明文，_p1 作为后续加密过程中需要用到的 key0，另一个 16 字节随机字符串作为 iv0，然后再进一步去调用 _gas 函数，使用 key0 和 iv0 加密 data，得到最终需要发回服务器的密文。

看起来很顺其自然，对吧？但是在抓包之后发现，最终传回服务器的只有密文，并没有客户端生成的 iv0。这就有点让人摸不着头脑了。众所周知，AES-CBC 是对称加密算法，加密和解密时需要使用相同的密钥和 IV。而采用这种方式进行密码传输，证明服务器存储了密码的明文，比对密码是在解密密文之后进行的。在没有 IV，只有密钥和密文的情况下，服务器是怎么做到验证密码正确性的呢？

在查阅了关于 AES-CBC 的资料，并请教了网安扛把子 Frank 同学之后，算是明白了这个过程。

AES-CBC

AES 分块加密中最基础的方式是 ECB（Electronic Code Book，电子密码本），该方式将明文分为一系列长度为 128 位（16 字节）的块（不足的则补齐至 128 位），然后分别对每一块进行加密，最后得到的所有分块即为密文。

由于在 ECB 模式下，相同的明文会产生相同的密文，这是不够安全的，因此后续诞生了 CBC、OFB、CTR 等其他模式。这里我们只讨论 CBC。CBC 全称 Cipher Block Chaining（密文分块链接），之所以叫这个名字，是因为这种在加密方式中，各个分块之间相互联系，像链条一样。其加密方法是，给定密钥 $K$ 和初始向量 $IV$，将明文 $P$ 同样分为一系列长度为 128 位的块（不足则补齐），记为 $P_0 \sim P_n$。记加密函数为 $E(P, K)$，其中 $P$ 是明文，$K$ 是密钥。将上述参量代入下列算法得到密文 $C$（记密文分块为 $C_0 \sim C_n$）：

$$C_0 = E(P_0 \oplus IV, K)$$

$$C_i = E(P_i \oplus C_{i +1}, K) (i > 0)$$

而 CBC 的解密方法则是加密的逆过程。给定密钥 $K$ 和初始向量 $IV$，将密文 $C$ 分为 $C_0 \sim C_n$ 块，记解密函数为 $D(C, K) $。将上述参量代入下列算法得到明文 $P$（记明文分块为 $P_0 \sim P_n$）：

$$P_0 = D(C_0 \oplus IV, K)$$

$$P_i = D(C_i \oplus P_{i -1}, K) (i > 0)$$

加密和解密过程的流程图如下所示：

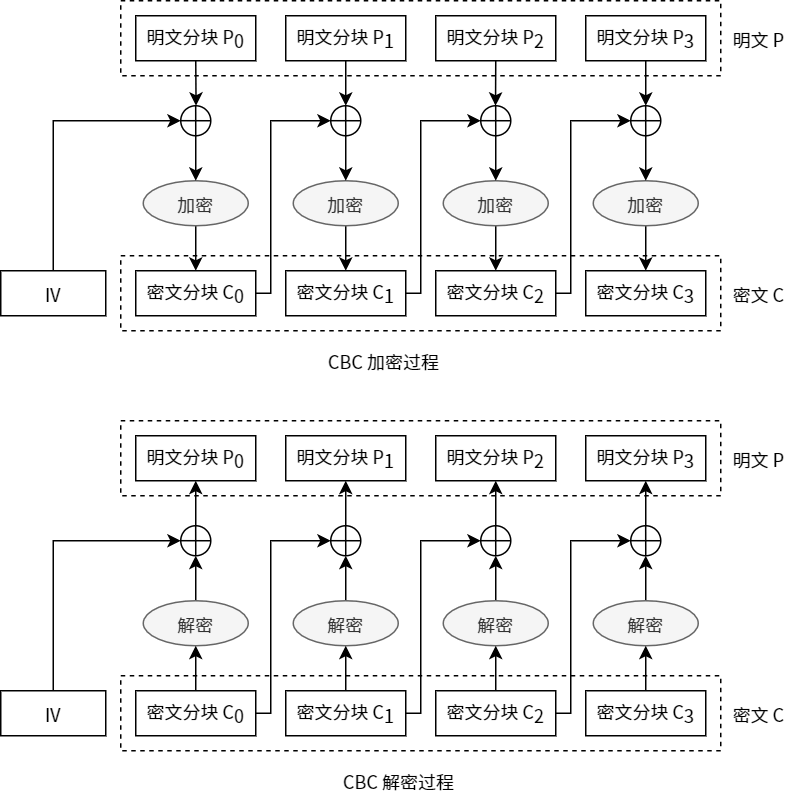
可以看到，IV 和密钥在加密解密的过程中都是必不可少的参量。那学校实现的加密方式是如何做到无需 IV 解密的呢？

分析学校的加密方法

从本文开头给出的代码可以看出，真正用于 AES 加密的明文，是前面补了 64 字节的密码，密钥是服务器生成的 _p1，IV 是随机的 16 字节。看起来并没有什么神奇的地方（真的吗）。既然瞪不出来，那我们就模拟一遍解密流程。

将补充的 64 字节随机数据分为 4 个 16 字节的块，记为 $R_0 \sim R_3$，后续密码明文记为 $P$（简单起见这里考虑密码只有一个块）。那么待加密的数据共计 5 个块，对应密文为 $C_0 \sim C_4$ 。密钥记为 $K$。已经解密但还没有进行异或运算的中间值记为 $T_i$。再强调一遍，解密过程是不知道 IV 的。

首先对于密文块 $C_0$，使用密钥 $K$ 进行解密后，得到中间数据 $T_0$。根据解密流程，可以得到这样一种关系： $T_0 = R_0 \oplus IV$。由于 $IV$ 是未知的，因此我们无法继续得出明文 $R_0$ 。

没关系，我们继续看下一个密文块 $C_1$ ，使用密钥 $K$ 进行解密后，中间数据 $T_1 = R_1 \oplus C_0$ 。注意到该式中 $T_1$ 和 $C_0$ 均已知，因此我们可以得到 $R_1 = T_1 \oplus C_0$ 。诶，明文居然出来了？

以此类推, $R_2$、$R_3$、$R_4$ 都可以计算出来。仔细观察可以发现，密文中的 $C_0$ 块，实际上充当了 $C_1 \sim C_4$ 这部分数据的 $IV$ 。因此，最终解密得到的明文是不包括原来的 $R_0$ 块的。

以下给出 C# 实现的加密和对应的解密算法：

static void Main(string[] args)
{
    Console.WriteLine(Encrypt("123", "1234567890123456"));
    Console.WriteLine(Decrypt("Uj+ILeid+NFwvGXa6mXe6SCqMHppLVFIocwJbRdo2pt111SSsrbaD6yl3d5/gsPggzhJZzG5AXVGVQkOHolrOk8yfpaf7bG6fJ9yek93pkY=","1234567890123456"));
}

/// <summary>
/// Do custom AES-ECB encryption for specified <paramref name="password"/> with <paramref name="salt"/>
/// </summary>
/// <param name="password">Password to be encrypted</param>
/// <param name="salt">Salt to be used as key</param>
/// <returns>A cipher string which is encoded using Base64</returns>
static string Encrypt(string password, string salt)
{
    var plain = Encoding.UTF8.GetBytes(GenerateSeed(64) + password);
    var key = Encoding.UTF8.GetBytes(new Regex("(^\\s+)|(\\s+\\$)").Replace(salt, ""));
    var iv = Encoding.UTF8.GetBytes(GenerateSeed(16));
    using var aes = new AesCryptoServiceProvider
    {
        Mode = CipherMode.CBC, Padding = PaddingMode.PKCS7, Key = key, IV = iv
    };
    using var encryptor = aes.CreateEncryptor();
    using var msEncrypt = new MemoryStream();
    using var csEncrypt = new CryptoStream(msEncrypt, encryptor, CryptoStreamMode.Write);
    csEncrypt.Write(plain);
    csEncrypt.FlushFinalBlock();

    return Convert.ToBase64String(msEncrypt.ToArray());
}

/// <summary>
/// Do custom AES-ECB decryption for specified cipher string <paramref name="c"/> with <paramref name="salt"/>
/// </summary>
/// <param name="c">Cipher string. Must be Base64 encoded</param>
/// <param name="salt">Salt to be used as key</param>
/// <returns>Original plain string. Note that this does not contains seed</returns>
static string Decrypt(string c, string salt)
{
    var cipherBytes = Convert.FromBase64String(c);
    var cipherContent = new byte[cipherBytes.Length - 16]; // Drop first 16 bytes
    Array.Copy(cipherBytes, 16, cipherContent, 0, cipherBytes.Length - 16);
    var key = Encoding.UTF8.GetBytes(new Regex("(^\\s+)|(\\s+\\$)").Replace(salt, ""));
    var iv = new byte[16];
    Array.Copy(cipherBytes, iv, 16); // Use first 16 bytes as IV for decrypting cipherContent
    using var aes = new AesCryptoServiceProvider
    {
        Mode = CipherMode.CBC, Padding = PaddingMode.PKCS7, Key = key, IV = iv
    };
    var decryptor = aes.CreateDecryptor();
    using var msEncrypt = new MemoryStream(cipherContent);
    using var csEncrypt = new CryptoStream(msEncrypt, decryptor, CryptoStreamMode.Read);
    using var srEncrypt = new StreamReader(csEncrypt);
    var decrypted = srEncrypt.ReadToEnd();

    return decrypted.Substring(16 * 3); // Drop first 48 bytes
}

static string GenerateSeed(int length)
{
    var ret = new StringBuilder();
    var tables = "ABCDEFGHJKMNPQRSTWXYZabcdefhijkmnprstwxyz2345678";
    for (var i = 0; i < length; i++)
        ret.Append(tables[Convert.ToInt32(Math.Floor(new Random().NextDouble() * tables.Length))]);

    return ret.ToString();
}

多说两句

这个加密方法看起来感觉挺神奇的，使用 CBC 相对来说提升了一定的密文破解难度，同时又避免将解密所需的参量全部通过网络传输。但这并不是最优解，实际工程中，通用的做法是使用非对称加密或者密钥交换协议，并配合 HTTPS。毕竟服务器上是不应该存储密码明文的。

另外，仔细观察可以发现，如果在原密码明文前只补充 16 字节随机数据的话，最终解密出来的数据直接就是密码——不过，显然这并不够安全。